В стремлении к максимальному реализму в метавселенной создание цифрового аватара с человеческим лицом, одновременно реалистичного и гибкого, остаётся ключевой задачей. Для её решения исследовательская группа из Швейцарской высшей технической школы Цюриха разработала технологию HyperGaussians. Она представляет собой своего рода «высокоразмерную эволюцию» трёхмерного гауссова распределения, которая делает тонкие выражения, блики, волосы и очки более чёткими и яркими.
С момента своего создания гауссово распределение (или разбрызгивание) стало одним из стандартов представления трёхмерных сцен благодаря скорости и качеству рендеринга. Его суть в использовании десятков тысяч небольших эллипсоидов, каждый из которых имеет цвет, прозрачность и трёхмерную ориентацию, для «забрызгивания» всей сцены, что в итоге даёт реалистичный рендеринг в реальном времени.
Однако в применении этой технологии для создания управляемых анимированных лицевых аватаров на основе монокулярных видео возникают узкие места. Существующие передовые методы, такие как FlashAvatar и MonoGaussianAvatar, обычно привязывают гауссовы точки к параметрической модели лица и используют нейронные сети для прогнозирования положения, поворота и смещения масштаба каждой гауссовой точки на основе параметров выражения лица.
Швейцарцы объясняют:
Это похоже на то, как если бы мы обтянули базовый скелет кожей, а затем с помощью нейронной сети слегка деформировали кожу. Но этот метод неэффективен при работе с крайне локальными и нелинейными изменениями.
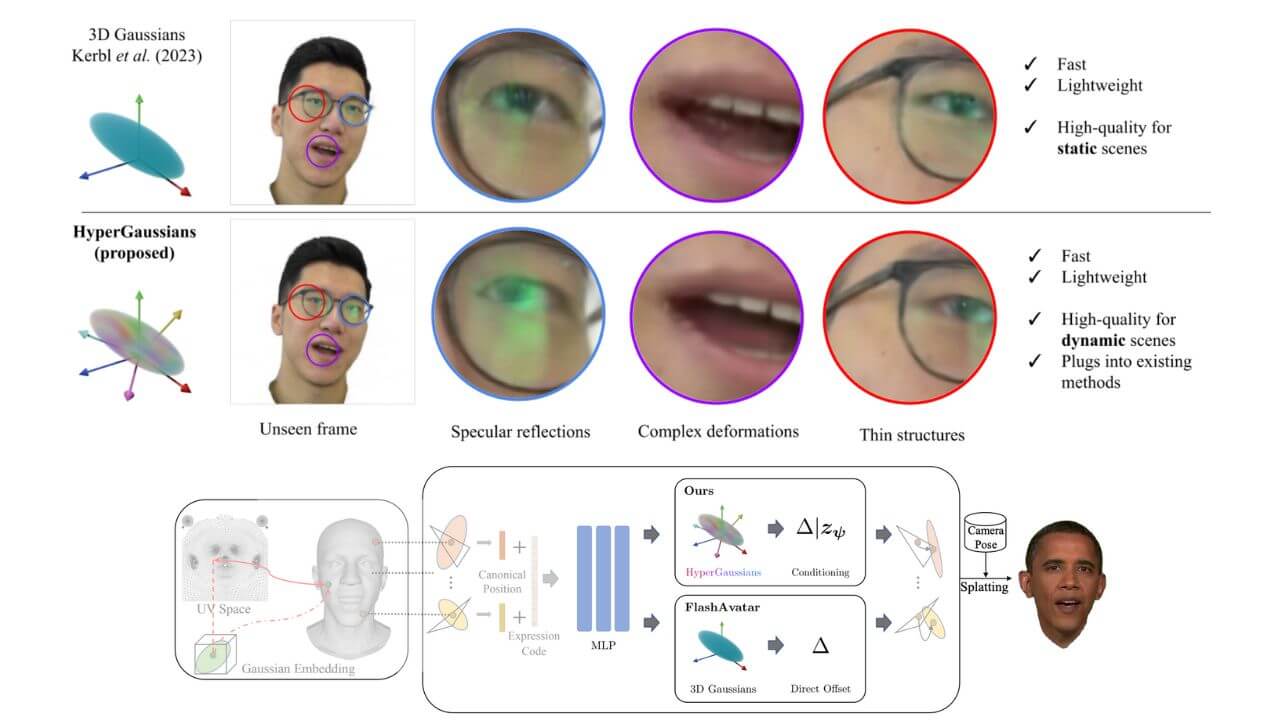
В итоге эти методы создают большие и размытые оправы очков, слипшиеся зубы, тусклые и некорректные блики на глазных яблоках и неестественные искажения при закрывании глаз.
Исследователи пришли к выводу, что проблема может заключаться не в сложности предсказательной сети, а скорее в верхнем пределе «выразительной силы» самого гауссова представления. Они подняли фундаментальный вопрос: что произойдёт, если не ограничивать гауссовы точки трёхмерным пространством, а вместо этого перенести их в пространство более высокой размерности?
Это основная концепция гипергауссианов. Она расширяет каждую традиционную точку гауссовой функции из трёхмерного эллипсоида в многомерное гауссово распределение в (m+n)-мерном пространстве.

Представьте себе традиционную трёхмерную гауссову матрицу как точку с тремя атрибутами: длиной, шириной и высотой. Гипергауссианы помещает эту точку, к примеру, в (3+8)-мерное. Три измерения — это привычные положение, поворот и масштаб (атрибутивные измерения), а новые восемь измерений (скрытые измерения) — это обучаемый «код внедрения», содержащий богатую локальную контекстную информацию.
Точка в этом многомерном пространстве представляет собой полное многомерное гауссово распределение с многомерным средним значением и ковариацией. При визуализации каждого кадра система вычисляет определённое 8-мерное «латентное состояние» для каждой точки гауссова распределения на основе текущих параметров выражения лица. Затем посредством математического процесса, называемого кондиционализацией, из этого многомерного гауссова распределения точно «нарезается» стандартная трёхмерная гауссова функция. Положение, форма и ориентация этой трёхмерной гауссовой функции динамически и точно корректируются в соответствии с текущим «латентным состоянием».
Это похоже на трансформер, который имеет бесчисленное множество возможных форм в многомерном пространстве (определяемом потенциальными измерениями) и может мгновенно трансформироваться в точную трехмерную форму, которая лучше всего подходит текущему состоянию в соответствии с различными инструкциями (параметрами выражения).
Однако высокоразмерные вычисления обычно сопровождаются огромными вычислительными затратами. В процессе «обучения» необходимо многократно вычислять обратную матрицу высокоразмерной ковариации, что практически невозможно при рендеринге в реальном времени.
Наибольший инженерный вклад исследовательской группы заключается в предложении «метода обратной ковариации». Они изменили математический подход, отказавшись от прямого манипулирования ковариационной матрицей и вместо этого манипулируя её обратной матрицей — матрицей точности. Это преобразование устраняет узкие места в вычислительных процессах, связанные с обработкой массивных матриц скрытых измерений, и позволяет обрабатывать лишь небольшие матрицы атрибутивных измерений.
В частности, независимо от потенциальной размерности — 8 или 128 — системе достаточно инвертировать лишь фиксированную малую матрицу размером 3×3 или 4×4. Этот метод повышает эффективность рендеринга многомерных гауссиан в сотни и более раз.
Чтобы показать универсальность и возможности системы, исследовательская группа интегрировала HyperGaussian и FlashAvatar, которую считают самой быстрой монокулярной системой видеоаватаров. Единственное изменение, которое они внесли, заключалось в замене выходных данных сети во FlashAvatar, предсказывающих гауссово положение точки, на выходные данные, предсказывающие кодировку «латентного состояния». Эта кодировка затем передавалась в модуль HyperGaussians, который генерировал окончательные условные смещения. Остальная часть модели осталась неизменной.
Количественный анализ пяти общедоступных наборов данных 19 разных людей, показал, что эта «минимально инвазивная» система достигла наилучших результатов по всем ключевым показателям.
Не менее убедителен скачок в визуальных эффектах:
- Тонкие структуры: оправы очков представляют собой не размытые цветные блоки, а чёткую геометрическую структуру; зубы отчетливы, между ними видны промежутки.
- Зеркальное отражение: блики на глазном яблоке могут естественно перемещаться в зависимости от угла обзора и выражения лица; отражение на линзе также становится более реалистичным.
- Сложные деформации: закрытие глаз происходит естественно и плавно, а нелинейные деформации, такие как оттягивание уголков рта, больше соответствуют физиологическим законам.
- Скорость сходимости: на ранних этапах обучения модель с гипергауссианами демонстрирует более чёткие детали, что свидетельствует о большей эффективности процесса оптимизации.


Команда также успешно интегрировала HyperGaussians в другую систему под названием GaussianHeadAvatar, добившись значительного улучшения визуального качества при увеличении времени обучения всего на 5,6%.
Успех HyperGaussians открывает важное направление: повышение выразительной силы базовых единиц представления часто даёт более существенные преимущества, чем наращивание сложности сетей. Исследователи рассчитывают, что новинка станет перспективным стандартным компонентом будущих систем динамического моделирования сцен. При этом команда подчеркнула риск злоупотребления технологией для создания дипфейков и призвала отрасль разработать руководящие принципы ответственного использования и этические стандарты.
Не пропускайте важнейшие новости о дополненной и виртуальной реальности — подписывайтесь на Голографику в Telegram, ВК и Twitter! Поддержите проект на Boosty.
Далее: Научный эксперимент поднял планку «ретинального» разрешения очков



