Учёные из Национального автономного университета Мексики и Монтеррейского технологического института сообщают о решении двухтысячелетней оптической проблемы Вассермана-Вольфа для линз любого размера. Их метод предполагает зависимость формы второй асферической поверхности от формы первой и фокусного расстояния, при этом вторая поверхность гасит сферические аберрации.
В устройствах с оптическими линзами края видимых через них изображений оказываются более размытыми, чем центр. Известное ещё грекам до нашей эры, это свойство было впервые аналитически описано лишь в 1949 году и получило название проблемы Вассермана-Вольфа по фамилиям давших описание учёных. Они же первыми нашли её решение, предложив использовать две асферические смежные поверхности. Применение их выкладок в производстве, однако, оказалось слишком дорогим, чтобы закрыть вопрос.
Группа латиноамериканских учёных в составе Рафаэля Гонсалеса-Акунья (Rafael G. González-Acuña), Гектора Чапарро-Ромо (Héctor A. Chaparro-Romo) и Хулио Гутьеррез-Вега (Julio C. Gutiérrez-Vegа) сформулировали собственное общее уравнение замкнутой формы для конструкции сферической линзы без аберраций. Оно уже получило название «уравнение Акуньи-Ромо».
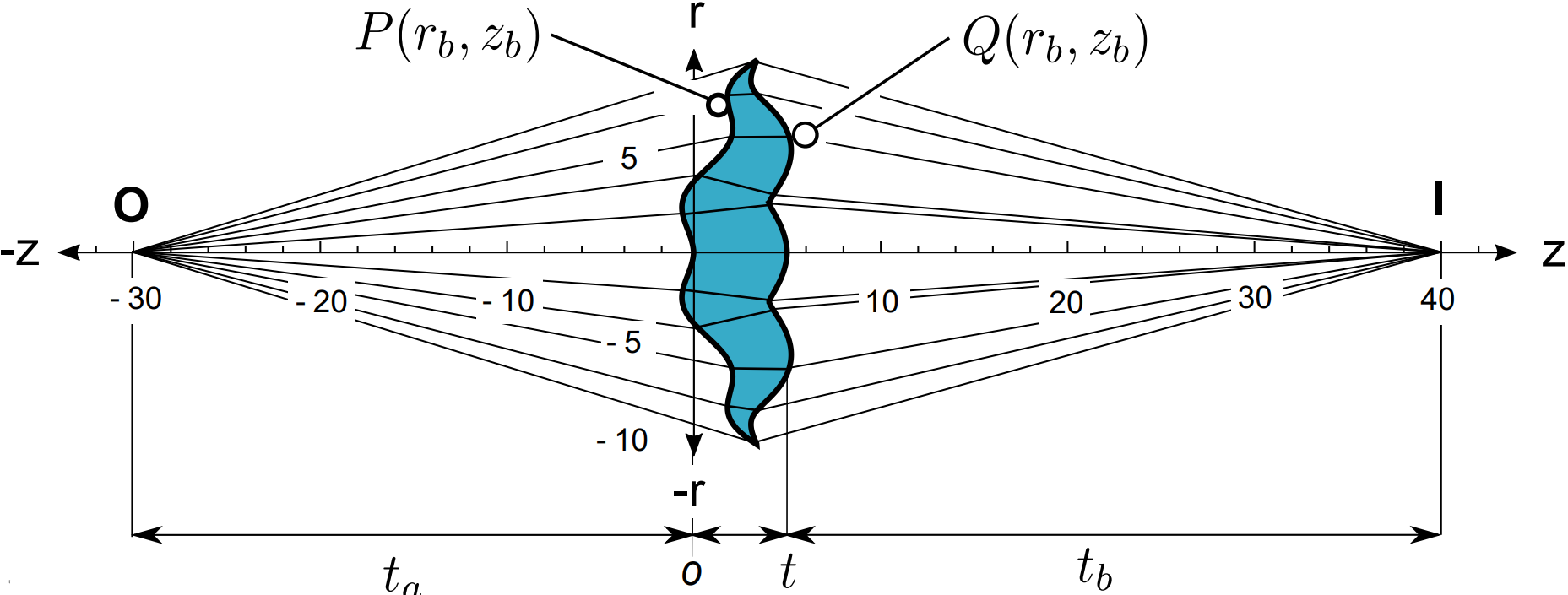
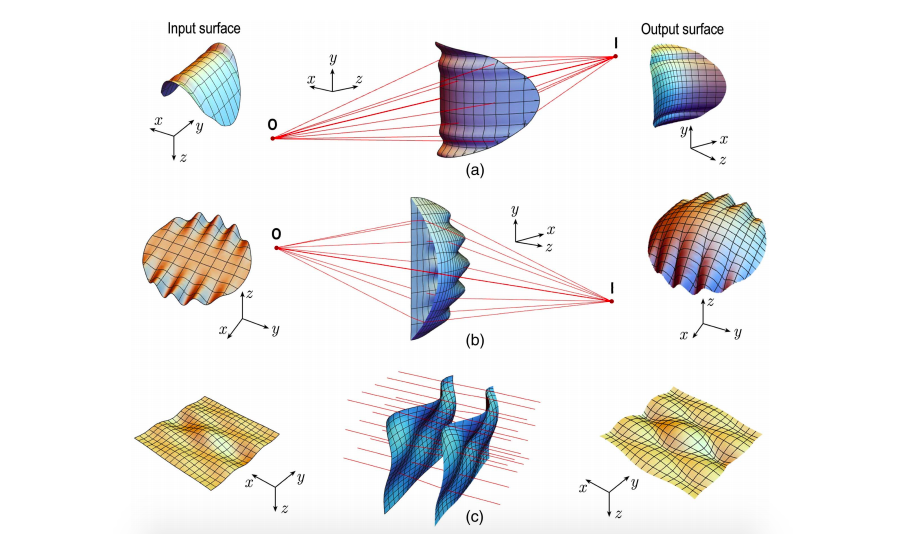
В этой статье мы рассмотрим случай, когда один из волновых фронтов свободной формы, а другой — сферический. Волновой фронт свободной формы генерируется первой поверхностью линзы, а сферический волновой фронт генерируется второй поверхностью. Кроме того, мы вводим выражение для закрытой формы для конструирования линз произвольной формы, свободных от сферической аберрации и астигматизма, что можно рассматривать как продолжение нашей работы. Формула даёт точное аналитическое уравнение выходной поверхности, учитывая произвольное выражение произвольной формы входной поверхности, чтобы исправить сферическую аберрацию и астигматизм, введённые первой поверхностью.
Вывод полностью аналитически основан на формальном применении вариационного принципа Ферма к стандартной геометрической оптике. В процессе выведения формулы мы применяем методологию проектирования, свободную от стратегий численной оптимизации. Мы проиллюстрируем применимость и надёжность формулы, продемонстрировав несколько типичных примеров проектирования с использованием очень сложных функций ввода, которые ранее не использовались в оптическом дизайне. Насколько нам известно, эта точная формула ранее не была представлена в литературе по оптическому дизайну.
По новой математической модели, говорят учёные, можно создавать линзы, точность передачи изображения через которые составляет 99,999999999999%. Формула может оказаться востребованной в производстве комплектующих для очков виртуальной и дополненной реальности, поскольку удешевляет производство оптики.
С выводами исследования вы можете познакомиться в оригинальной статье.
Не пропускайте важнейшие новости о дополненной, смешанной и виртуальной реальности — подписывайтесь на Голографику в Telegram, ВК, Twitter и Facebook!
Далее: Facebook скрестила линзы для ВР-очков



